Ground expression
In mathematical logic, a ground term of a formal system is a term that does not contain any variables at all, and a closed term is a term that has no free variables. In first-order logic all closed terms are ground terms, but in lambda calculus the closed term λ x. x (λ y. y) is not a ground term.
Similarly, a ground formula is a formula that does not contain any variables, and a closed formula or sentence is a formula that has no free variables. In first-order logic with identity, the sentence 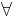 x (x=x) is not a ground formula.
x (x=x) is not a ground formula.
A ground expression is a ground term or ground formula.
Contents |
Examples
Consider the following expressions from first order logic over a signature containing a constant symbol 0 for the number 0, a unary function symbol s for the successor function and a binary function symbol + for addition.
- s(0), s(s(0)), s(s(s(0))) ... are ground terms;
- 0+1, 0+1+1, ... are ground terms.
- x+s(1) and s(x) are terms, but not ground terms;
- s(0)=1 and 0+0=0 are ground formulae;
- s(z)=1 and ∀x: (s(x)+1=s(s(x))) are expressions, but are not ground expressions.
Ground expressions are necessarily closed. The last example, ∀x: (s(x)+1=s(s(x))), shows that a closed expression is not necessarily a ground expression. So, this formula is a closed formula, but not a ground formula, because it contains a logical variable, even though that variable is not free.
Formal definition
What follows is a formal definition for first-order languages. Let a first-order language be given, with the  the set of constant symbols,
the set of constant symbols,  the set of (individual) variables,
the set of (individual) variables,  the set of functional operators, and
the set of functional operators, and  the set of predicate symbols.
the set of predicate symbols.
Ground terms
Ground terms are terms that contain no variables. They may be defined by logical recursion (formula-recursion):
- elements of C are ground terms;
- If f∈F is an n-ary function symbol and α1, α2, ..., αn are ground terms, then f(α1, α2, ..., αn) is a ground term.
- Every ground term can be given by a finite application of the above two rules (there are no other ground terms; in particular, predicates cannot be ground terms).
Roughly speaking, the Herbrand universe is the set of all ground terms.
Ground atom
A ground predicate or ground atom is an atomic formula all of whose terms are ground terms. That is,
If p∈P is an n-ary predicate symbol and α1, α2, ..., αn are ground terms, then p(α1, α2, ..., αn) is a ground predicate or ground atom.
Roughly speaking, the Herbrand base is the set of all ground atoms, while a Herbrand interpretation assigns a truth value to each ground atom in the base.
Ground formula
A ground formula or ground clause is a formula all of whose arguments are ground atoms.
Ground formulae may be defined by syntactic recursion as follows:
- A ground atom is a ground formula; that is, if p∈P is an n-ary predicate symbol and α1, α2, ..., αn are ground terms, then p(α1, α2, ..., αn) is a ground formula (and is a ground atom);
- If p and q are ground formulae, then ¬(p), (p)∨(q), (p)∧(q), (p)→(q), formulas composed with logical connectives, are ground formulae, too.
- If p is a ground formula and we can get q from it that way some ( or ) we delete or insert in the p formula, and then the result, q is well-formed and equivalent with p, then q is a ground formula.
- We can get all ground formulae applying these three rules.
References
- Dalal, M. (2000), "Logic-based computer programming paradigms", in Rosen, K.H.; Michaels, J.G., Handbook of discrete and combinatorial mathematics, p. 68
- Hodges, Wilfrid (1997), A shorter model theory, Cambridge University Press, ISBN 978-0-521-58713-6
- First-Order Logic: Syntax and Semantics